미국의 수학경시대회 -(1)
미국수학협회 (The Mathematical Association of America)는 미국 초중고교생의 수학능력을 높이기 위해 매년 수학경시대회 (American Mathematics Competitions; AMC)를 개최하고 있다.
1950년 5월 11일 뉴욕 메트로폴리탄에서 처음 열린 AMC는 뉴욕 지역의 238개 학교에서 6천 명의 학생들이 참여하며 큰 성공을 거뒀다. 이후 매년 6천 개 이상의 학교에서 30만 명 이상의 학생들이 참가하는 명실공히 미국을 대표하는 최고의 수학 경시대회가 되었음은 물론 국제적으로도 그 권위를 인정받고 있다.
AMC는 수험생의 나이와 학년 그리고 실력에 따라 다음과 같은 대회로 구분된다.
▶ AMC 8: 4학년부터 출전기회가 주어지고, 8학년 이하의 학생들이 응시하는 대회
▶ AMC 10: 10학년 이하의 학생들이 응시하는 대회
▶ AMC 12: 12학년 이하의 학생들이 응시하는 대회
▶ AIME: American Invitational Mathematics Examination, AMC 10과 AMC 12 시험에서 상위 성적을 기록한 만명 정도의 학생들이 초대되어 치르는 시험
▶ USAJMO: United States of America Junior Mathematical Olympiad, AMC 10 시험에서 고득점을 올린 학생들을 초대해 국제 주니어 수학 올림피아드 대회에 참가할 미국 대표를 선발하기 위해 치르는 대회
▶ USAMO: United States of America Mathematical Olympiad, AIME 고득점자들을 초대해 국제 수학 올림피아드 대회에 참가할 미국 대표를 선발하기 위해 치르는 대회
AMC 8은 1985년, AMC 10는 2000년, AMC 12는 1950년, AIME는 1983년, USAMO는 1972년에 각각 시작되었다. 수학 분야와 관련한 최고의 특별활동 중 하나인 미국 수학 경시대회(AMC) 는 수상 경력은 물론 입상을 하지 못하더라도 참가를 준비하는 과정을 대학 입학 원서를 쓸 때의 에세이 소재로도 많이 활용한다. 수학에 대한 열정과 관심 그리고 도전 정신을 어필할 수 있는 좋은 소재이기 때문이다.
이번 호에서는 미국 수학경시대회 AMC의 첫 단계 'AMC 8'에 대해서 소개한다.
AMC 8이란?
AMC 8은 문제 해결 능력의 개발을 촉진하기 위해 25개의 다지선다형 중학교 수학 문제를 40분 동안 푸는 객관식 수학 시험이다. 8학년 이하의 학생들에게 분석적 사고와 수학에 대한 긍정적인 태도를 개발할 기회를 제공한다.
각 문항의 점수는 모두 같고, 틀린 문제는 감점이 없으며 정답 숫자만큼만 점수로 계산한다. 문제지와 답안지가 분리되어 있고, 문제지에는 풀이 과정 등을 기입할 수 있으나 정답으로 간주되지는 않으며, 답안지에 정답으로 표시한 답만 정답으로 인정된다.
시험이 끝나면 학생들은 답안지뿐만 아니라 문제지도 감독관에게 제출해야 한다. 또한 학생들은 출제된 문제나 정답을 직접적으로 언급해서는 안되며, 인터넷이나 기타 미디어를 통한 언급도 금지되어 있다.
25개 문항은 중학교 레벨의 수학 개념을 이용해야 하는 비교적 난이도가 높은 문제들로 구성되어 있다. 학교에서는 하나의 수학 개념을 배운 뒤 1단계 정도의 변형을 거친 문제들을 다루었다면 AMC 8 경시대회 문제는 2단계 이상의 사고 과정을 거쳐야 정답을 맞힐 수 있는 문제들로 이루어져 있다. 시험범위는 보통 Algebra 1과 Geometry이고, 문제의 범위는 대략 확률(probability), 통계(estimation), 비율(percentages), 도형 (geometry 피타고라스의 정의 포함), 공간 지각(spatial visualization), 실생활 문제, 그래프를 읽고 해석하는 문제 등 단순 계산 문제부터 사고력을 많이 요구하는 문장제(word problem) 문제까지 다양하게 출제된다.
AMC 8은 프랑스어, 스페인어 그리고 시각 장애인을 위해 대형 프린트와 점자로도 치를 수 있다.
AMC 10부터는 출제 범위도 광범위해지고 미국 수학 올림피아드(USAM) 출전권에 영향을 미치기 때문에 시험준비를 탄탄히 해야 하지만, AMC 8은 수학에 관심이 있거나 평소 수학을 잘한다고 생각하는 학생이라면 별도의 준비를 하지 않았어도 한번 치러 볼 것을 추천한다.
결과가 좋지 않더라도 좋은 경험이 될 수 있어 수학을 공부하는데 도움이 될 뿐 아니라 다음해에 또 응시해도 되기 때문에 자신의 능력을 점검하는 기회로 삼아 볼 수 있다.
그러나 AMC 8에서 좋은 성적을 거두었다 하더라도 그 위 단계인 AMC 10이나 AMC 12, AIME, USAMJMO, USAMO 출전 자격과는 무관하다. 오직 AMC 10과 AMC 12의 결과에 따라서 AIME, USAMJMO, USAMO에 초대된다.
AMC 8을 준비하고자 하는 학생은 기출문제를 중심으로 공부하면 도움이 된다. 기출문제집과 해답지는 미국 수학 협회 AMC 웹사이트 https://www.maa.org/press 에서 판매하고 있고, www.amc.edfinity.com 에서 온라인 코스를 등록하면 기출문제를 중심으로 공부할 수 있다.
AMC 8 참가 자격은 시험 당일 기준으로 14세 반 이하의 학생이라면 지원할 수 있지만, 일반적으로 6, 7, 8학년 학생들에게 추천하고, 4, 5학년 학생도 수학에 자신이 있다면 도전해 볼 수 있다.
AMC 8은 1년에 한 번 11월에 치러지는데 지난 2018년도에는 11월 13일에 치러졌고 올해 시험 일정은 아직 발표 되지 않았다. 시험이 끝나면 12월 중순쯤 시험결과가 집으로 배달된다.
등록비로 120불 정도의 비용이 소요되며, AMC 컨테스트 계정을 만들어 온라인으로 등록할 수도 있고 우편이나 팩스로 보낼 수도 있다. 온라인으로 등록하면 $10이 할인된다.
영어가 부족한 학생들은 사전(전자사전이 아닌 일반사전)을 이용할 수 있으나, 처음 치르는 시험에만 사전 지참이 허용되고 두 번째 시험부터는 사전을 사용할 수 없다. 그러므로 미리미리 수학 용어를 영어로 숙지해 두어야 한다. 시험에 사용할 사전은 시험 시작 24시간 전에 감독관에게 제출해야, 감독관은 사전에 문제가 없는지 조사한 뒤, 시험이 시작되면 학생에게 다시 돌려준다. 그리고 다른 학생들에게 사전을 이용하는 학생들에 대해 반드시 공지해야 한다.
계산기는 2007년을 마지막으로 더 이상 사용할 수 없는데, AMC에 따르면 더 이상 계산기가 필요한 문제는 출제되지 않기 때문이라고 한다.
AMC 8의 목적
AMC8은 미국 수학경시대회 시리즈의 입문 단계로 더 높은 단계로 올라가기 위해 기초를 다지는 계기가 된다. 즉, 중학교 수학 과정에 나오는 내용들을 확실하게 습득하고 경시대회에서 응용해 봄으로써 기초를 탄탄히 다질 수 있는 계기가 되는 것이다. 학생들은 스스로 수학에 얼마나 자신이 있는지, 앞으로 계속해서 경시대회에 출전해도 괜찮을지, 출제되는 문제가 학교에서 배우는 내용과 어떤 차이가 있는지 확인해 보는 계기로 활용하면 된다.
또한, AMC 10의 문제 경향을 미리 가늠해보는 기회가 될 수 있으며 앞으로 다루게 될 어려운 문제에 대한 두려움을 없앨 수 있는 기회로 삼을 수 있다.
또 다른 목적은 고등학교에 진학하기 전, 중학생들에게 도전 정신을 갖게 하는 한편 수학에 대한 열정과 긍정적 태도를 가지며, 수학에 흥미를 느껴 계속해서 수학을 공부하려는 관심을 불러 일으키기 위함이다.
AMC 8 어워드
지난해 11월 13일에 치러진 2018년 AMC 8 에는 미 전역 1844개의 학교에서 98,448명이 참가했으며 이 중 45명이 만점을 받았다.
만점을 받은 학생에게는 'Certificate of Distinction'이 수여 되고, 출전한 각 학교에서 가장 높은 점수를 획득한 학생에게는 'AMC 8 Winner Pin'이 주어진다..
또 만점을 받은 학생과 상위 1퍼센트 안에 속한 학생에게는 Distinguished Honor Roll Certificate(2018년 1326명)를, 상위 5퍼센트내의 학생들에게는 AMC 8 Honor Roll Certificate(2018년 5033명)를 수여한다.
각 학교의 상위 3명에게는 각각 금, 은, 동 Certificate of Outstanding Achievement 이 주어지며, 6학년 이하의 수험생 중 15점 이상을 획득한 학생들은 'Achievement Roll' 그룹에 해당되어 'AMC 8 Merit Certificate'을 받게 된다.
AMC 8은 25점 만점으로 매년 달라지기는 하지만 대략 20점 이상이 Distinguished Honor Roll 으로 상위 1퍼센트에 해당하고, 15점~19점 사이가 Honor Roll 그룹에 속하는 것이 보통이다.
AMC 8 예제
다음은 AMC 웹사이트에서 제공하는 AMC8 경시대회 예제들이다.
---------------- 비율(Percentages) -----------------
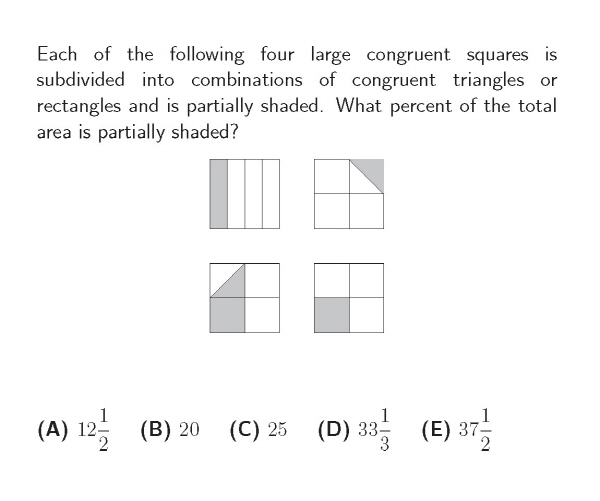
▶ 정답: C (난이도 중)
▶ 풀이: 오른쪽 상단의 사각형과 왼쪽 하단의 사각형의 회색부분을 합치면 25퍼센트이고 나머지 다른 두 사각형의 회색 부분도각각 25퍼센트이므로 4개의 사각형을 합친 전체 영역에 대한 회색 부분의 영역 비율 역시 25퍼센트가 된다.
▶ 정답: 180과 594를 소인수 분해 (prime factorization)를 하면 이다. 여기서 180과 594의 최소공배수는 이고, 최대 공약수는 이므로, 최소 공배수와 최대 공약수의 비율은 이 되어 정답은 330이다.
----------------- 실생활 관련 문제 ------------------
▶ 풀이: 반 파운드의 생선이 50% 세일 후 3불 이므로 세일 전 가격은 6불이다. 반 파운드가 6불이면 한 파운드는 두 배인 12불이 된다.
--------------------- 단순연산 ----------------------
▶ 풀이: 먼저 괄호 안의 등식에서 패턴을 찾는다. 숫자들 두 개씩 묶었을때 합이 항상 1인것을 알 수 있다. -1+ 2는 1, - 3 +4는 1 이런식으로 패턴이 지속되었을 때 마지막 숫자가 1000이므로 그것의 반 500이 괄호 안의 등식에 대한 답이 되고 결국 4x500은 20,000이다.
▶ 정답: B (난이도 중)
▶ 풀이: 먼저 각각의 등식에서 지수인 p, r, s의 값을 구한 다음 곱하는 것이 포인트.
첫번째 식에서 3의 4제곱은 81 이므로 가 되고 3외 2제곱은 9가 되므로 p는 2. 두번째 식에서는 가 되고 2의 5제곱이 32이므로 r은 5. 세번째 식에서는 가 되고 6의 4제곱이 1296이 므로 s는 4. 따라서 2x5x4은 40이다.
----------------- 확률(Probability) ------------------
▶ 풀이: 간단한 확률이므로 모든 경우의 수를 나열한다. 동전의 '앞앞앞', '앞앞뒤', '앞뒤앞', '앞뒤뒤', '뒤앞앞', '뒤앞뒤', '뒤뒤 앞', '뒤뒤뒤' 로 총 8개의 경우 중, 앞면이 최소 2번 연속적으로 나오는 경우는 '앞앞앞', '앞앞뒤', '뒤앞앞' 3번이다.
----------------- 도형(Geometry) ------------------
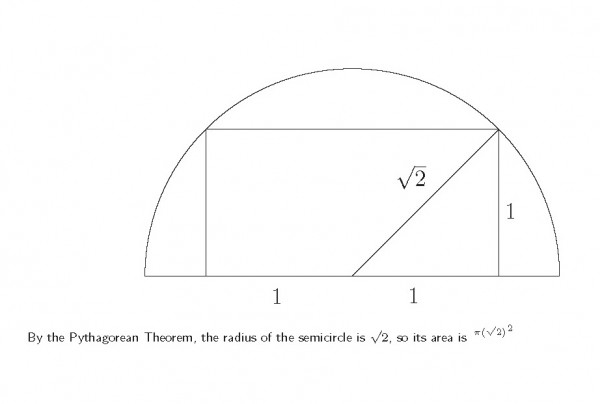
▶ 풀이: 문제에서 등장하는 두 도형 , 사각형과 반원의 관계를 이해하고 그림으로 그리는 것이 첫 단계 이다. 사각형의 긴 면이 반월의 직경에 접하므로 아래와 같은 그림을 그린 후 , 짧은면이 1이고긴 면이 2이므로 그의 반은 1이 되어 작은 직각이등변삼각형이 그려진다.
피타고라스의 정리에 의해 직각 이등변 삼각형의 긴2 변은 √2가 되고, 반원에서 보면 √2가 반지름이므로 원의 공식 에 대입하면 가 되고, 반원이므로 그의 반인 π가 된다.
▶ 풀이: 제일 작은 반원의 넓이가 8π이므로 원넓이 공식 ()에 의해 지름, 즉 AB의 길이는 8이다. AC를 지름으로 하는 반원의 둘레가 8.5 π이므로 원 둘레 (2πr) 에 의해 지름, 즉 AC의 길이는 17이다. 그렇다면 삼각형의 다른 면인 BC의 길이는 피타고라스의 정리에 의해
의 등식이 성립되어 BC의 길이는 15이고 그 길이의 반인 7.5 가 BC를 지름으로 하는 반원의 반지름이 된다.
---------- 공간지각(Spatial Visualization) ----------
▶ 풀이: 단순히 가로, 세로의 길이가 60개와 32개의 이쑤시개가 아니라 정사각형의 눈금을 만들어 가며 이쑤시개를 연결하는 것이 이 문제의 포인트다. 따라서 가로의 길이가 60개의 이쑤시개라면 33의 이쑤시개가 세로로 같이 사용되고, 세로의 길이가 32개가 되려면 가로로 61개의 이쑤시개가 함께 사용된다. 따라서 (60x33) + (32x61)의 등식이 성립한다.