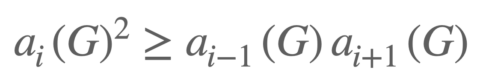허준이 교수가 해결한 11개 수학 난제들은?
수학 분야의 노벨상, ‘필즈상’
미국 프린스턴대 수학과 교수 겸 한국 고등과학원 석학 교수인 허준이 교수는 한국 시각으로 2022년 7월 5일 오후 4시경 수학 분야 최고 권위상인 필즈상을 수상했다.
필즈상(Fields Medal)은 4년마다 세계수학자대회에서 수여하는 메달로 1936년 제정된 후 한 대회에서 2~4명까지 수상하기에 올해까지 수상자가 총64명밖에 되지 않는다. 노벨상에 수학 분야가 없는 관계로 수학 분야의 노벨상으로도 불리는 필즈상은 아벨상, 울프상과 함께 수학 분야 최고권위의 상으로 불리운다.
한 가지 특이한 점은 다른 상과 대비되는 제한 조건이 있다는 점이다. 바로 40세 미만에게만 수여된다는 점인데, 상의 제안자인 캐나다 수학자 필즈는 이에 관해 필즈상은 이미 이루어진 업적을 기리기 위해 수여하지만, 이와 동시에 장래에도 계속 좋은 성과를 낼 수 있도록 장려하는 의미로 상을 수여한다고 밝힌 바 있다.
허준이 교수의 연구 분야는?
먼저 허준이 교수의 연구 분야는 조합 대수기하학(Combinatorial Algebraic Geometry)으로 방정식들로 정의되는 기하학적 공간을 연구하는 대수 기하학을 통해서 조합론의 문제를 해결하는 비교적 새로운 수학 분야이다.
허준이 교수는 조합 대수기하학을 통해 여러 조합론 난제(보통 추측 conjecture의 형태로 제시됨)를 해결하고, 대수기하학의 새로운 지평을 연 공로를 인정받아 필즈상을 수상하게 되었다. 허준이 교수는 그동안 어떤 조합론의 난제를 해결했을까? 또한 이는 수학적으로 어떠한 의미를 갖고 있을까?
허준이 교수가 해결한 난제로는 리드 추측, 호가 추측, 메이슨-웰시 추측, 로타 추측, 다울링-윌슨 추측, 강한 메이슨 추측, 브리로스키 추측, 도슨-콜번 추측, 오쿤코프 추측, 딤카-파파디마 추측, 엘리아스-프라우드풋-웨이크필드 추측 등이 있다.
리드 추측을 시작으로 호가 추측, 메이슨-웰시 추측, 로타 추측 등 여러 난제 해결
허준이 교수는 서울대학교에서 석사과정을 마친 후, 미국 일리노이주립대학 박사 과정에 입학했다. 허 교수는 박사 과정 중 수학계 난제 중 하나인 리드 추측(Read’s conjecture, 1968)을 해결했다고 알려져 있다. 리드 추측은 영국의 수학자 로날드 리드가 1968년 제시한 문제로, 그래프에서 인접하는 꼭짓점에 서로 다른 색을 색칠하는 경우의 수인 채색 다항식(chromatic polynomial) 계수의 절댓값이 갖는 성질에 대한 추측을 말한다. 또한, 호가 추측(Hogger, 1974)은 이들이 로그-오목성을 가진다는 추측을 말한다.
참고로, 양수인 실수로 이루어져 있으며 작은 수로부터 시작하여 정점에 도달한 후 줄어들기 시작하는 수열이(줄어들다가 다시 커지지 않고 단 하나의 정점만 존재, 즉 봉우리가 하나인 수열: 아래로 오목한 곡선 혹은 단봉 unimodal 이라고 부름) 로그를 취했을 때, 다시 이런 수열이 된다면 ‘로그 오목성(log-concavity)’을 띈다고 한다. 즉, 로그-오목은 특정 부등식(아래)이 모든 i에 대해 성립하는지 묻는 것을 말하는 것이다.
허 교수는 그의 예전 스승 히로나카 헤이스케 서울대 석좌교수의 특이점 이론을 그래프에 적용하는 방법을 발견했으며 위 방법을 이용하여 리드 추측을 해결하게 된다. 위 증명으로 허 교수는 주목을 받아 그의 소속을 미시간대학 박사 과정으로 옮기게 된다. 그는 이곳에서 리드 추측이 속한 더 큰 문제인 로타 추측(Rota-Heron-Welsh conjecture, 1971)에 도전하게 된다.
로타 추측이란 이탈리아 태생의 미국 수학자 잔카를로 로타가 1971년 리드-호가의 추측(Read’s conjecture, 1968 그리고 Hoggar, 1974)과 메이슨-웰시의 추측을 일반화하여, 임의의 매트로이드(matroids) M에 대해 특성 다항식의 계수들이 로그-오목임을 보이는 문제이다.
메이슨-엘시 추측(Mason-Welsh conjecture, 1971)은 유한 차원의 벡터 공간에 포함된 유한개의 벡터 집합 E가 주어질 때, 원소가 i개인 E의 부분 집합 중 일차 독립인 것의 개수를 나타내는 수열에서 이러한 특정 다항식의 계수들 즉, 특정 수열이 로그-오목인지에 관해서 묻는 문제이다. 또한 강한 메이슨 추측(strong Mason conjecture, 1972)은 메트로이드의 독립 수열에 관해서 묻는 문제이다.
리드 추측이 그래프 채색 다항식의 성질을 밝히는 문제였던 점에 반해, 로타 추측은 벡터 공간에 있는 유한 집합의 특성 다항식의 계수들이 로그-오목임을 보이는 보다 일반적인 문제이다. 허 교수는 영국의 수학자 윌리엄 호지가 개척한 대수기하학 관련 연구(호지-리만 관계 혹은 호지 이론)를 통해서 위 문제를 해결했다.
“Top-heavy” 다울링-윌슨 추측도 해결하다
다울링-윌슨 추측(Dowling-Wilson conjecture, 1974)은 1974년 수학자 토마스 다우링과 리차드 윌슨이 제시한 문제로 “top-heavy” 문제라고도 불리운다. d차원 공간에 있는 점 n개가 초평면 하나에 모두 포함되지 않는다면 (가정: 2d ≥ 직선 p일 때), 그 점으로 결정되는 (p-1) 차원 공간의 수는 점 n개로 결정되는 (d-p) 차원 공간의 수보다 클 수 없다는 추측이다 (엄상일 교수의 따끈따끈한 수학에서 발췌).
허 교수와 위스콘신대학교 매디슨 캠퍼스 왕 교수는 위 추측에 대한 증명뿐 아니라 각각의 (p-1) 차원 공간이 대응되는 (d-p) 차원 공간에 포함될 수 있도록 대응시킬 수 있다는 내용을 밝혀서 화제가 되었다.
브리로스키 추측, 도슨-콜번 추측 역시 로그-오목 관련 추측
브리로스키 추측 (Brylawski conjecture, 1982)는 1982년 수학자 토마스 브리로스키가 제시한 문제로 연결된 매트로이드의 텃 다항식(Tutte polynomial: 유한 그래프 및 유한 매트로이드에 대응되는 2변수 정수 계수 다항식) 이 기약(irreducible: 더 낮은 차수의 다항식의 곱으로 표시되지 않음)할 수 있다는 추측이다. 도슨-콜번 추측 (Dawson-Colbourn conjecture, 1984) 역시 브리로스키 추측과 같이 특정 다항식에서 나오는 로그-오목과 관련이 있는 추측이다.
도슨은 매트로이드의 h-vector가 로그-오목이라고 추측했으며 콜번은 네트워크 안정성(network reliability)의 맥락에서 그래픽 매트릭스에 대해서 로그-오목임을 추측했다. 허 교수는 Denham, Garrousian 및 Schulze의 특정 다항식에 대한 기하 공식을 기반으로, 특정 필드에 대해 표현할 수 있는 매트로이드에 대해서 도슨의 추측을 증명해냈다.
허준이 교수의 연구는 계속된다
오쿤코프 추측(Okounkov conjecture, 2003)은 러시아의 수학자 안드레이 유례비치 오쿤코프가 2003년 불변량 이론(invariant theory)의 관점에서 로그-오목임을 추측한 이론이다. 이외에도 허 교수가 해결한 난제로는 딤카-파파디마 추측(Dimca-Papadima conjecture, 2003: 수학자 알렉산드루 딤카와 슈테판 파파디마가 추측한 이론으로 고립된 특이점을 가진 모든 호말로이드 초표면 homaloidal hypersurfaces 에 관한 추측), 그리고 엘리아스-프라우드풋-웨이크필드 추측(Elias-Proudfoot-Wakefield conjecture, 2016: 매트로이드에 대해서 Kazhdan-Lusztig 다항식을 도입하며, 다항식이 평면 격자의 각 요소 쌍에 대해서도 정의될 수 있다는 이론) 등이 있다.
허준이 교수의 연구 분야인 조합론은 컴퓨터 계산, 인공 지능 등에 활발히 활용되고 있다. 또한 현재의 많은 산업과 강한 연계성을 보이고 있기에 전망도 매우 밝다고 할 수 있다. 허준이 교수와 Quanta Magazine의 인터뷰에 따르면 그는 수학자들은 계속해서 아름다운 결과를 만들 것이라고 확신한다고 밝힌 바 있다. 필즈상의 의의대로 허준이 교수의 장래에 계속 아름다운 성과가 나오길 기대해 본다.